初めに
現場の計画業務や割り当て業務では、「経験がある人ほど上手くできる」、「試行錯誤しながら何とか調整している」という状況が少なくありません。一方で、
- 人によって計画の品質がばらつく
- 制約が増えるほど調整に時間がかかる
といった課題も、多くの現場で共通して見られます。こうした課題の背景には、「判断基準が暗黙知になっている」「全ての制約を同時に考慮するのが難しい」といった構造的な問題があります。
数理最適化は、これらの判断基準や制約を数式として整理し、機械的に最適な解を導くことで、属人化や試行錯誤といった課題を解決することができます。
本記事では、
- 数理最適化とは何か
- どのような課題に向いているのか、
- AI・機械学習との関係
を整理します。
この回を読み終えたときに、「数理最適化が自分の業務に使えるかもしれない」と感じてもらえると幸いです。
数理最適化とは
数理最適化とは
数理最適化とは
制約条件を満たす解(実行可能解)のなかで目的関数の値が最小あるいは最大になるもの(最適解)を求める問題
のことです。
もう少し噛み砕くと、
- 守らなければならない条件(制約条件)があり
- その範囲の中で
- 「一番良い選択」を数学的に決める
ための考え方・技術が数理最適化です。
数理最適化は 数理計画問題、数理計画法とも呼ばれます。
物流、製造、シフト作成、在庫管理など、計画や割り当てが必要な業務で幅広く使われています。
直観的な例
例えば、次のような状況を考えてみます。
- トラックには積載量の上限がある
- 複数の荷物を運ばなければならない
- できるだけ少ない台数で運びたい
このとき、
- 「積載量を超えてはいけない」 → 制約条件
- 「使うトラック台数を最小にする」 → 目的関数
となります。
人間が経験や勘で調整してきたこの判断を、数式とアルゴリズムで再現可能な形にするのが数理最適化です。
数理最適化が有効な課題
次のような特徴をもつ課題に対して、数理最適化は有効です。
- 選択肢の数が多い
- 制約条件が多い
- 「最良」を数値で定義できる
選択肢の数が多い
数理最適化は、選択肢の組み合わせが膨大な問題を扱うのが得意です。
例えば、
- 荷物をどのトラックに載せるか
- 作業員をどの時間帯に配置するか
- どの順番で作業や配送を行うか
といった問題では、
選択肢が少し増えるだけで組み合わせは爆発的に増えます。
人間は直感的に「良さそうな案」を選ぶことはできますが、すべてのパターンを比較することは不可能です。
数理最適化では、膨大な組み合わせを探索し、その中から条件を満たす解を効率的に見つけ出します。
制約条件が多い
現場の計画業務では、「こうしたい」という希望だけでなく、「守らなければならない条件」が数多く存在します。
例えば、
- トラックごとに積載量や積める荷物の種類が決まっている
- 作業員ごとに勤務時間や対応可能な作業が異なる
- 法令・安全ルール・社内ルールを満たす必要がある
- 特定の作業は順番を守らなければならない
といった制約です。
これらの制約は、1つ1つは単純でも、同時に満たそうとすると急激に難しくなります。
人間は一部の重要な制約に注目して調整することはできますが、
- 気づかないうちに制約を破ってしまう
- 後から修正が必要になり、やり直しが増える
といったことが起こりがちです。
数理最適化では、すべての制約条件を明示的に定義し、「守られない解」は最初から除外した上で探索を行います。
そのため、
- 制約漏れによる手戻りを防げる
- 制約が増えても、調整の考え方を変える必要がない
という点で、制約の多い問題ほど効果を発揮します。
「最良」を数値で定義できる
数理最適化が使えるかどうかを分けるポイントの1つは、「何を最も良い状態とするか」を明確に定義できるかです。
例えば、
- 総移動距離を最小にする
- コストを最小にする
- 利益を最大にする
- 遅延時間を最小にする
といった形で、「最小化」「最大化」が数値で表せる場合、数理最適化が有効です。
逆に、
- 何となくバランスが良い
- ベテランの感覚ではこちらが良い
といった評価は、そのままでは扱えません。
ただし、「評価基準を数値化できる」、「優先順位を重みとして表現できる」場合には、数理最適化に落とし込めることも多くあります。
数理最適化の対象となりうる課題
上記のように、数理最適化は
- 選択肢の数が多い
- 制約条件が多い
- 「最良」を数値で定義できる
といった特徴をもつ課題の解決に向いています。
もし、現場で
- 試行錯誤に時間がかかっている
- 本当に最適かわからない
と感じている業務があれば、それは数理最適化の対象となり得ます。
AI・機械学習・数理最適化の関係
AIとは
AI(Artifitial Intelligence、人工知能)は、
人間の思考プロセスと同じような形で動作するプログラム、あるいは人間が知的と感じる情報処理・技術のこと
です。
人間が行っている知的活動として、判断・推論・認識・学習のようなものがあります。これらの知的活動をコンピューター上で実現する仕組みが、広くAIと呼ばれます。
機械学習とは
機械学習(Machine Learning、ML)とは、
人間の学習に相当する仕組みをコンピューター等で実現するものであり、一定の計算方法(アルゴリズム)に基づき、入力されたデータからコンピューターがパターンやルールを発見し、そのパターンやルールを新たなデータに当てはめることで、その新たなデータに関する識別や予測等を可能とする手法
です。
機械学習の代表的な学習方式は、次の3つに大別されます。
- 教師あり学習
-
正解データ(ラベル)を与えて学習する方法
- 教師なし学習
-
正解を与えず、データの構造や分布を見つける方法
- 強化学習
-
行動の結果として得られる報酬を最大化するよう学習する方法
機械学習は、AIを構成する主要な技術領域のひとつです。
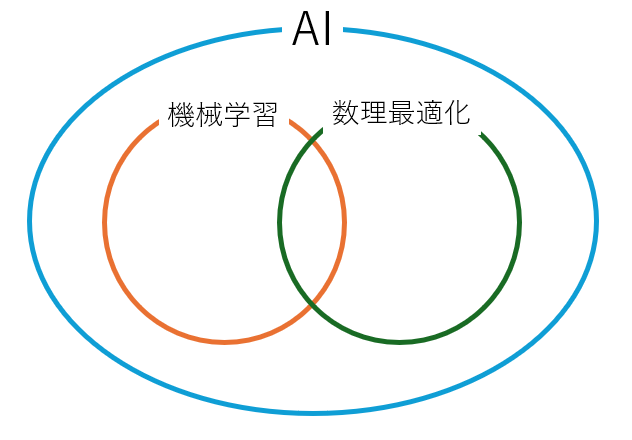
AI・機械学習・数理最適化の関係について
機械学習・数理最適化はいずれもAIを構成する重要な技術領域です。機械学習、数理最適化は簡単に言うと
- 機械学習
- 「データからルールやモデルを学習する」技術
- 数理最適化
- 「定義された制約のもとで最良の意思決定を行う」技術
でした。
これらは独立な関係ではなく、
- 機械学習の学習過程に数理最適化の知見を用いる
- 数理最適化に強化学習(機械学習の1つ)の手法を用いる
といったように相互に補完しあう関係にあります。
まとめ
本記事では、次の点を解説しました。
- 数理最適化は、「制約条件のもとで最良の意思決定を行う」ための考え方であること
- 選択肢や制約が多く、最小化・最大化といった形で良し悪しを数値化できる課題と相性が良いこと
- 数理最適化はAI・機械学習とは役割が異なり、制約と目的に基づいて判断や計画を論理的に決める技術であること
- 機械学習と組み合わせることで、互いに補完し合いながら実務で力を発揮する関係にあること
これらを通じて、数理最適化が現場の業務や意思決定に活用できそうだ、というイメージを持ってもらえれば幸いです。
補足・参考
AI、機械学習の定義について
AIの定義は現在も統一されていません。本記事のAI、機械学習の定義は総務省が出している「令和元年版 情報通信白書」の説明を引用しています。

コメント